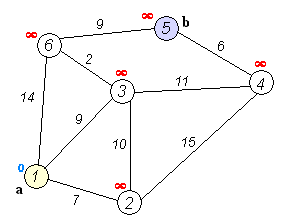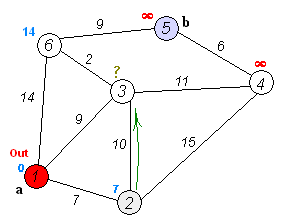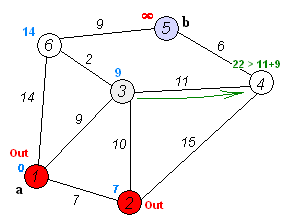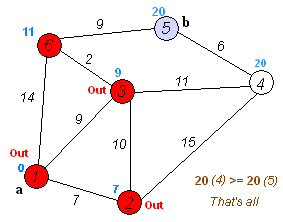
The key idea in Dynamic Programming (DP) is to generate a set of subproblems from a larger problem, and then use recursion or a bottoms up approach to combine the subproblem results to solve the original problem.
Recursion lends itself nicely to DP as the program stack itself becomes the mechanism to generate, traverse and combine the subproblems, and memoization is used to prevent re-solving the same subproblem if there’s overlap.
Let’s think about the classic recursive Fibonacci algorithm.
def fib_rec(n):
if n<2: return n
return fib_rec(n-1) + fib_rec(n-2)
The subproblems is calculating each number as the sum of the prior two. We use the program stack to generate these nodes depth first, with the base cases being the numbers in positions 0 and 1. Combing these sub-results is straightforward – we add them all the way back up the stack.
Now we just have to optimise with memoization to prevent re-calculating nodes.
def fib_dyn(n,memo={}):
if n<2: return n
if len(memo)>n:
return memo[n]
else:
fibn = fib_dyn(n-1,memo) + fib_dyn(n-2,memo)
memo[n] = fibn
return fibn
DP can also be done without recursion, via a bottoms up approach while adhering to the same principles.
def fib_bot_up(n):
f=[]
for k in range(n+1):
if k<2: f.append(k)
else: f.append(f[k-1]+f[k-2])
return f[k]
You can see that in the bottoms up approach we start with the base cases, and move up the sub-results until we get to the desired position in the sequence. We could optimize further by keeping track of only the prior two numbers in our loop.
Let’s think about another simple problem: Let’s say you can climb a staircase of n steps by one or two or three steps at a time. How many ways are there to get to the top?
First, let’s think about the subproblems. We’ll call step zero as the top step – the base case. Once I’m there, there’s only one way to climb the staircase. From any step, I can get to the top by adding the ways to get to the top from 1 step up, 2 steps up and 3 steps up from where I am. Like the Fibonacci sequence, these subproblems can be nicely generated by the program stack using recursion.
def countways_rec(n):
if n<0: return 0
if n==0: return 1
return countways_rec(n-1)+countways_rec(n-2)+countways_rec(n-3)
Now we add memoization:
def countways_dyn(n,memo={}):
if n<0: return 0
if n==0: return 1
if len(memo)>n:
return memo[n]
else:
return countways_dyn(n-1,memo)+countways_dyn(n-2,memo)+countways_dyn(n-3,memo)
Now a bottoms up approach. Again, we start with the base case and build up from there. We can keep a lookup table to keep track of the previously calculated values that we’re building our final result on.
def countways_bottomsup(n):
lookup = {}
lookup[0]=1
lookup[1]=1
lookup[2]=2
for step in range(3,n+1):
lookup[step]=lookup[step-1]+lookup[step-2]+lookup[step-3]
return lookup[n]
These are the basic principles of all DP problems. Figuring out the subproblems, and how to generate and combine them can get trickier in some problems. I’ll explore some of these in subsequent posts.
For completeness, here’s a solution of the steps problem with a variable number of steps that can be jumped.
def countways_bottomsup_varjumps(n,jumps):
lookup = {}
lookup[0]=1
for step in range(1,n+1):
lookup[step]=0
for jump in jumps:
if step-jump >= 0: lookup[step]=lookup[step]+lookup[step-jump]
return lookup[n]