This post uses python and Dijkstra’s algorithm to calculate the shortest path given a start node (or vertex), an end node and a graph. The function will return the distance from the start node to the end node, as well as the path taken to get there.
The implementation below sticks pretty closely to the algorithm description in the wikipedia entry, which I turned into something a little more pseudo-code-ish to help me implement it:
Initial state:
1. give nodes two properties - node.visited and node.distance 2. set node.distance = infinity for all nodes except set start node to zero 3. set node.visited = false for all nodes 4. set current node = start node.
Current node loop:
1. if current node = end node, finish and return current.distance & path 2. for all unvisited neighbors, calc their tentative distance (current.distance + edge to neighbor). 3. if tentative distance < neighbor's set distance, overwrite it. 4. set current.isvisited = true. 5. set current = remaining unvisited node with smallest node.distance
Here’s my implementation – it’s recursive, as suggested by the algorithm description:
import sys
def shortestpath(graph,start,end,visited=[],distances={},predecessors={}):
"""Find the shortest path btw start & end nodes in a graph"""
# detect if first time through, set current distance to zero
if not visited: distances[start]=0
# if we've found our end node, find the path to it, and return
if start==end:
path=[]
while end != None:
path.append(end)
end=predecessors.get(end,None)
return distances[start], path[::-1]
# process neighbors as per algorithm, keep track of predecessors
for neighbor in graph[start]:
if neighbor not in visited:
neighbordist = distances.get(neighbor,sys.maxint)
tentativedist = distances[start] + graph[start][neighbor]
if tentativedist < neighbordist:
distances[neighbor] = tentativedist
predecessors[neighbor]=start
# neighbors processed, now mark the current node as visited
visited.append(start)
# finds the closest unvisited node to the start
unvisiteds = dict((k, distances.get(k,sys.maxint)) for k in graph if k not in visited)
closestnode = min(unvisiteds, key=unvisiteds.get)
# now take the closest node and recurse, making it current
return shortestpath(graph,closestnode,end,visited,distances,predecessors)
graph = {'a': {'w': 14, 'x': 7, 'y': 9},
'b': {'w': 9, 'z': 6},
'w': {'a': 14, 'b': 9, 'y': 2},
'x': {'a': 7, 'y': 10, 'z': 15},
'y': {'a': 9, 'w': 2, 'x': 10, 'z': 11},
'z': {'b': 6, 'x': 15, 'y': 11}}
print shortestpath(graph,'a','a')
print shortestpath(graph,'a','b')
print "\nExpected Result:\n(0, ['a'])\n(20, ['a', 'y', 'w', 'b'])"
As you can see I turned the example in wikipedia into a graph for the test case in the code above:
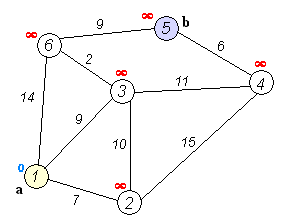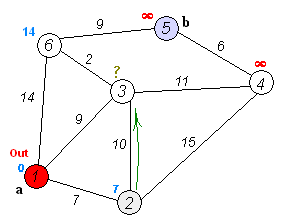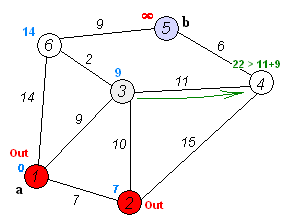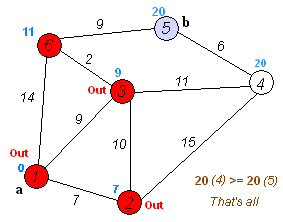
I also found this useful about how to represent and process graphs in python: http://ftp.ntua.gr/mirror/python/doc/essays/graphs.html. I think this was written by Guido himself.
There’s a bunch of interesting implementations on the web, including two here. Faster and more elegant perhaps, but it took me a little longer to understand them.

Hey there,
I was wondering… This looks pretty cool and I’d like to know how to make it work with cities and distances like this:
NewYork Chicago 200
Chicago LA 100
Chicago SanFrancisco 1000
SanFrancisco Florida 1400
END
NewYork
Florida
This means, that the distance from NewYork to Chicago is 200, Chicago to LA is 100, etc. Note: Chicago to NewYork is unknown we only know NewYork to Chicago.
Then the user inputs ‘END’ and in each line the starting city and finishing city, respectively.
f = []
while True:
a = raw_input()
if a == ‘FIM’:
break
f.append(a)
city1 = raw_input()
city2 = raw_input()
This would work and create an array with all of them.
My question is how to “Convert” that array to a dictionary usable by this function?
Here’s an example of how the array would be:
NewYork Chicago 200
Chicago LA 100
Chicago SanFrancisco 1000
SanFrancisco Florida 1400
[‘NewYork Chicago 200’, ‘Chicago LA 100’, ‘Chicago SF 100’, ‘SF Florida 1400’]
Thanks much for your time.
Can I get your email address, I need help to find out maximum capacity path from a source node to all other nodes.
I think you have a bug:
If start == end at first iteration:
print shortestpath(graph,’a’,’a’)
Traceback (most recent call last):
File “./shortpath.py”, line 39, in
print shortestpath(graph,’a’,’a’)
File “./shortpath.py”, line 13, in shortestpath
return distances[start], path[::-1]
KeyError: ‘a’
You need to init distances[] before enter while() loop.
Thanks Int-0
Now fixed.
Dip
my email address is in the about page of the blog.
You should use float(“inf”) (aka python’s infinity) instead sys.maxint (a fixed value). Remember in python ints are automatically parsed to longs when required, so you can raise easily maxint on a graph without overflows.
if i want all shortest path.
How to edit this?
There is a bug in your code.
Using mutable objects as default values in your function definition may cause it to execute correctly only the first time it is called in a program, any subsequent calls that receive different input data may fail or return incorrect values.
This is because the function arguments that are mutable objects will carry over their contents to subsequent calls of this function if those arguments are omitted, they are not initialized to the default values in your function definition, as you are intending. The default values of mutable objects are only used when the function is first called in a program.
This behaviour is by design, see-
http://bugs.python.org/issue4181
and
http://bugs.python.org/issue4619
This behaviour can be avoided by not relying on the default argument values when calling the function, ie. always include all argument values that are mutable.